Into the MMIX MOR instruction
I recently finished reading the first three volumes of Donald Knuth’s infamous "The Art of Computer Programming" (TAOCP) series. The first three volumes were published nearly back-to-back in the late 60's/early 70’s, but although they were always planned as part of a larger work, Knuth put the series on hold for nearly 30 years before publishing the next volume which was just released a few years ago. You might expect that to be called "volume 4", but volume 4 is so large that he split it into three books of their own: volume 4A, 4B and 4C. Of course, with a 30-year gap between publications, a bit of a break in continuity is expected — and although he's put a lot of effort into retaining the style and spirit of the earlier books, one big difference is immediate as soon as you pick up the book: MMIX.
Being a series of books about programming, the set includes quite a bit of example code — Knuth chose to present all of the sample code not in a commercial programming language but instead in assembler. Not just any assembler language, though – one that he made up just for the book. The first three volumes were written using a fictitious assembler language that he called MIX. However, having been designed in the late 60’s, it looks like the assembler languages of the day. Before publishing the next volume, he conceded that MIX was "showing its age" and revamped the entire thing into a more modern RISC-style assembler that he name "MMIX".
One interesting and unexpected inclusion in Knuth's MMIX assembly language are the MOR and MXOR instructions that treat their inputs as matrices of single bits and perform linear algebra-style matrix multiplications against them. To the best of my knowledge, no commercially available microprocessor has ever implemented such an instruction; there are some implementations like Intel's MMX that cover some special cases, but nothing (as far as I can tell) as general-purpose as MOR and MXOR are.
The MMIX specification defines MOR as treating each bit of each input register as a discrete
element and performing a classic matrix multiplication on the implied matrix. Registers are 64 bits
each, so the dimensions of each bit matrix are 8x8 and the output 8x8 binary matrix takes the form
for i = 0..7. Note that the ordinary row and column
ordering is inverted here; you'd expect rows to come first and columns to come after; Knuth defines
mor as mT($X) = mT($Y) & mT($Z). Although it's not called
out specifically in the book, I think that it's defined this way because Z can be specified as
a constant (albeit a one-byte constant) whereas Y can't.
o[r][c] = or/xor(a[c+i]*b[r+i])
Being as I am, much more programmer than mathematician, I had to implement an emulator to make sense of these instructions and their use; Knuth himself, being as much mathematician as programmer, is adept at finding clever uses of this sort of matrix multiplication to quickly handle some interesting corner cases, but I had to see them work myself before I could start to understand them.
You could, of course, build MOR and MXOR in hardware (that's the point, after all) so that the result would be computed in a single clock cycle. A simplified 16-bit MOR circuit is illustrated in figure 1, below. MXOR could be implemented by replacing the OR gates on the right-hand side with XOR gates, and a full 64-bit circuit as called for by the MMIX specification could be built by using 4 times as many logic gates and circuits (although a real hardware designer would have to be called in to solve the attenuation problem you'd probably run into if you implemented this many branches from a single input).
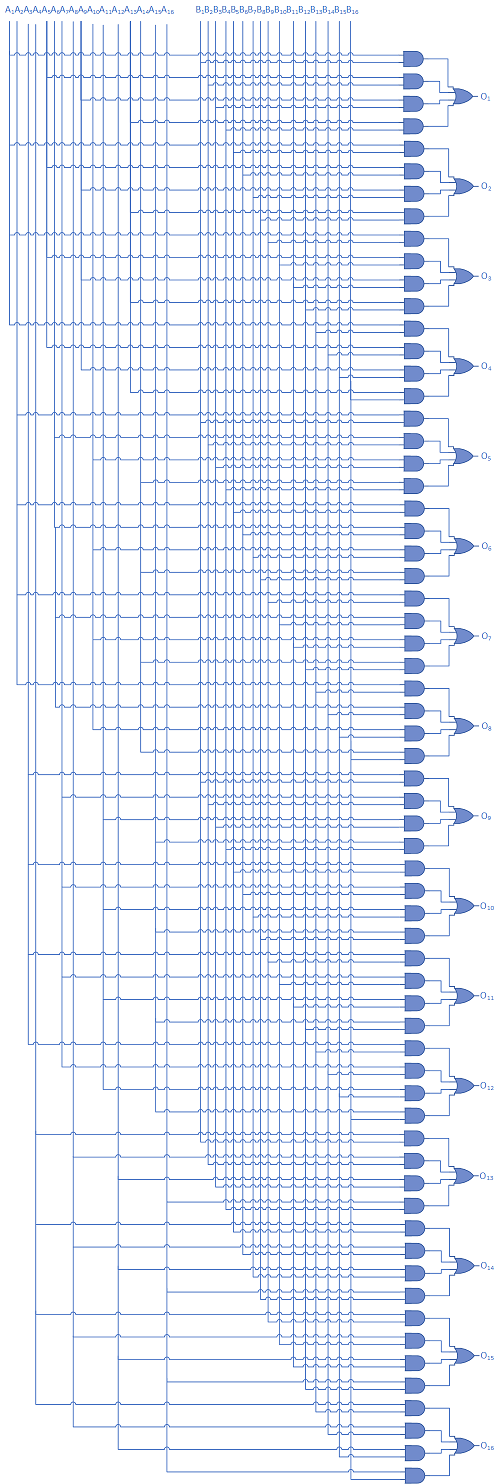
Figure 1: A simple 16-bit MOR circuit
In software, though, it makes more sense to go ahead and code the actual matrix multiplication loops. A basic matrix multiplication of integer arrays in C looks like the one in figure 2, below.
aint mat_mult(int a[], int b[], int o[], int m, int n, int p) {
int r, c, i;
for (r = 0; r < m; r++) {
for (c = 0; c < p; c++) {
o[r*m+c] = 0;
for (i = 0; i < n; i++) {
o[r*m+c] += a[r*m+i] * b[i*n+c];
}
}
}
}
Figure 2: General integer matrix multiplication
(Note that this supports the more general matrix multiplication case where the arrays are of different sizes
as long as the "vertical" dimension of the first matrix matches the "horizontal" dimension of the
second). Translating that to binary operation is pretty straightforward; first I have to change the
indexing to select individual bits rather than array elements and then change the addition and
multiplication operations to ands and ors (or xors). The description of
mor calls for the input matrices to be transposed and the output to be transposed before
being returned; again, it's quicker to just transpose the matrices "in place".
long mor(unsigned long a, unsigned long b) {
int r, c, i;
unsigned long o = 0L;
unsigned long bit;
for (r = 0; r < 8; r++) {
for (c = 0; c < 8; c++) {
bit = 0L;
for (i = 0; i < 8; i++) {
bit |=
(a & (1L << (r * 8 + i))) >> (r * 8 + i) &
(b & (1L << (i * 8 + c))) >> (i * 8 + c);
}
o |= bit << (r * 8 + c);
}
}
return o;
}
Figure 3: Bit Matrix operations
Here, I'm just replacing the indexing operations with bit shifting and masking (I've also hardcoded
the "inner index" n since it can only ever be 8). Selecting and combining
bits from the input is just a little tricky — I have to left shift to select just the bit I want
to operate on, but then I have to shift that back to the right so that the & operator works
correctly. If I didn't do that, I'd be AND-ing unaligned bits, and the output would
always be zero. Otherwise, this lines up pretty closely with the general matrix multiplication
operation above in figure 1. Here I'm OR-ing the bits; MXOR could be
simulated by replacing the middle |= with ^=.
There are various complex matrix multiplication routines that speed up a general matrix multiplication
operation by exploiting some of the algebraic properties of addition and multiplication.
Unfortunately, since the
logic operators of mor don't obey those same properties, you can't apply those same
speed ups to this code. If you look closely at figure 2, though,
you'll notice that I'm actually doing everything "backwards" — since my indices are counting
from 0 to 8, I end up working from LSB to MSB. Since each bit is independent of each other bit,
it doesn't matter what "order" you compute them in. In fact, you can even compute multiple bits at
a time, which Knuth himself exploits in his own mor
implementation. Figure 4, below, shows the "official" MMIX
implementation of mor (which he calls bool_mult), with the
typedefs included.
typedef enum {false, true} bool;
typedef unsigned int tetra;
typedef struct {
tetra h, l;
} octa;
octa zero_octa;
octa shift_right(octa y, int s, int u)
{
while(s>=32)
y.l= y.h,y.h= (u?0:-(y.h>>31)),s-= 32;
if(s) {
register tetra yhl= y.h<<(32-s),ylh= y.l>>s;
y.h= (u?0:(-(y.h>>31))<<(32-s))+(y.h>>s);
y.l= yhl+ylh;
}
return y;
}
octa bool_mult(octa y, octa z, xor) {
octa o,x;
register tetra a,b,c;
register int k;
for(k = 0, o = y, x = zero_octa; o.h || o.l; k++, o = shift_right(o,8,1))
if(o.l&0xff) {
a= ((z.h>>k)&0x01010101)*0xff;
b= ((z.l>>k)&0x01010101)*0xff;
c= (o.l&0xff)*0x01010101;
if(xor)
x.h^= a&c,x.l^= b&c;
else
x.h|= a&c,x.l|= b&c;
}
return x;
}
Figure 4: Official MMIX MOR implementation
In this way, he exploits this parallelism to compute a mor result in 8 (instead of the
512) loop iterations that figure 3 takes. (His is faster, but you have to admit mine is easier to
read).
It's pretty surprising the uses that he's able to put it to. For instance, MOR-ing an
(8-byte) register with 0x0180402010080402 emulates the x86 instruction ROR MMIX does have an
equivalent native instruction. In the same way, he can insert blanks in between bytes (for instance,
to convert ASCII to UTF-16) by skipping every other byte. Maybe some day we'll see an actual hardware
implementation of mor/mxor and I can put this study to practical use, but
in the meanwhile, it's fascinating to study even as a theoretical exercise.
Add a comment:
Completely off-topic or spam comments will be removed at the discretion of the moderator.
You may preserve formatting (e.g. a code sample) by indenting with four spaces preceding the formatted line(s)

