How LZW (GIF) Compression Works
Last April, I posted a description of the GZIP compression algorithm, which is itself mostly based on Abraham Lempel and Jacob Ziv's LZ'77 [1] algorithm. I won't rehash all of it here, but the gist of the algorithm is that, as you scan forward through a document you'd like to compress, you search backwards in the document for the longest match of the exact same text as you've scanned. If you find a match then, rather than outputting the text of the match itself, you output a "back pointer" to the match along with the length of the match.
One issue in the implementation of LZ'77 algorithm is exactly how to encode these back pointers. The GZIP/DEFLATE algorithm originally developed by Phil Katz as part of his PKZIP software uses a clever Huffman coding to efficiently represent these backpointers inline with actual text. Lempel and Ziv followed up their seminal 1977 paper with what is now known as LZ'78 [2] which solves this problem in a different way. Rather than storing backpointers to longest matches, the LZ'78 algorithm instead looks for repeating sequences and assigns codes to these. What is output by the compressor are just these codes; the decompressor turns codes back into sequences. In 1984, Terry Welch suggested some performance improvements that, although they don't change the basic nature of the LZ'78 algorithm, make it run quite a bit faster and compress better. Compuserve chose this algorithm as the compression method used in the .GIF image format; this is still how GIF files are encoded. I'll examine the details of Welch's LZW (Lempel-Ziv-Welch) [3] algorithm here.
In general, LZ'78 and LZW fall into a family of compression algorithms known as "dictionary" algorithms. The codes that represent potential matches are called dictionary entries. You can think of this as a real-world implementation of a "perfect" compression algorithm that assigns a code to each word that occurs in the source document and outputs only the codes for these words. Of course, there are three problems with this theoretical approach:
- The entire document would need to be scanned in order to build the dictionary in the first place, and then scanned again to output the compressed representation. This makes it impossible to apply this method to a data stream, and slows down compression even if re-scanning the document is feasible.
- The compressor would need to be aware of what constituted a "word" in the source document. Even for English text, this isn't necessarily obvious; although the compressor could just consider each space-delimited token as a word, it would end up missing potential opportunities to assign codes to common two-word pairs such as "at the" or "in order". If the document wasn't English text — say, something as exotic as an image — deciding what constitutes a word is even more complex.
- The dictionary itself would need to be transmitted with the compressed document so that the decoder would be able to successfully decompress it. This would almost definitely defeat the purpose of the compression in the first place.
LZ'78 solves these problems by treating every two-byte sequence in the document as a dictionary entry. If two bytes are encountered which are already in the dictionary, then the code is output and a new, three-byte, dictionary entry is created which consists of the discovered dictionary entry along with the subsequent byte. If this dictionary entry is encountered, its code is output and a new dictionary entry is created.
It's clear how this approach solves the problem first two problems - the dictionary is built in real time, and the codes are output as matches are encountered and it's not necessary to re-scan the document to compress it. Since sequences of bytes are considered matches rather than "words", this technique can be applied to any document.
What's not necessarily obvious is how this solves the last problem - the decompressor needs to have access to the dictionary in order to actually recover the original text. The real beauty of LZW is that the dictionary and the compressed output are intertwined in such a way as to allow the decompressor to recreate the dictionary as it is inflating the compressed data stream. In this way, the compressor transmits only the compressed output — the dictionary indices themselves — and the decompressor regenerates the dictionary on the fly as it decompresses.
How this actually works is best illustrated with an example. Take the
first line of the book of Genesis as an example:
in the beginning God created the heavens and the earth.
The compression function starts by initializing the first 256 entries of
the dictionary to the 256 possible bytes:
char **dictionary;
...
// pre-initialize the first 255 entries with their own values
for ( dictionary_ind = 0; dictionary_ind < 256; dictionary_ind++ )
{
dictionary[ dictionary_ind ] = ( char * ) malloc( 2 );
sprintf( dictionary[ dictionary_ind ], "%c", dictionary_ind );
}
Listing 1: Dictionary initialization
Here, I've implemented the dictionary as an array of char *
pointers; each entry in the dictionary is a string. (Ignore for the moment
that I haven't initialized the dictionary itself; I'll come back to that).
Now that the dictionary has been initialized, start reading the input, one byte at a time. The first byte is 'i'. Search the dictionary for the longest match that matches the current input pointer. Since the dictionary currently contains only one-byte strings, the match will occur at position 105: the ASCII code for the letter 'i'. The compressor outputs the index of this match (which happens to be the ASCII code for the first byte of input, but you should consider this "coincidental").
Now, move on to the next byte. Again, the longest match is found in the dictionary at position 110, the ASCII code for 'n'. However, since two consecutive bytes have been seen, they are added to the dictionary, so there's a new dictionary entry 'in'. Now the dictionary contains:
| index | value |
|---|---|
| 0 | 0 |
| ... | |
| 0x69 (105) | 'i' |
| ... | |
| 0x6E (110) | 'n' |
| ... | |
| 0xFF (255) | 255 |
| 0x100 (256) | 'in' |
in the beginning God created the heavens and the earth.
^
and the dictionary contains the following strings:
| 0x100 (256) | 'in' |
| 0x101 (257) | 'n ' |
| 0x102 (258) | ' t' |
| 0x103 (259) | 'th' |
| 0x104 (260) | 'he' |
| 0x105 (261) | 'e ' |
| 0x106 (262) | ' b' |
| 0x107 (263) | 'be' |
| 0x108 (264) | 'eg' |
| 0x109 (265) | 'gi' |
Now, however, the dictionary is scanned for the longest match of the
input string 'inning God created the heavens and the earth'. This time,
the longest match isn't found at the entry corresponding to the ASCII
code of the current byte, but instead at entry 256: 'in'. Now, the compressor
outputs this entry and moves on to the next byte. When it does, though,
it doesn't add 'in' to the dictionary again, but instead adds 'inn' at entry
267. You can now begin to see how this algorithm actually ends up compressing
its input; the dictionary is built up over time and contains longer and
longer matching strings.
The compressor moves on and encounters another 'in' match at position 13. Again, this matches entry 256; but not the new entry 267 (which was 'inn'). However, since a match was found, the dictionary gets an entry of 'ing'. This continues on for a while without finding a match until position 28:
in the beginning God created the heavens and the earth.
^
Now you can see where LZW is sub-optimal (as in, it's not perfect). A "perfect" compressor would recognize that the 5-byte sequence ' the ' has been encountered before, at position 3. LZ'77 does, in fact, recognize exactly this. LZW, however, is more deterministic. All it recognizes is that the two-byte sequence ' t' has been seen before and outputs the code 258, and adds ' th' to its dictionary. Over time, though, as it keeps encountering ' the ' in the input stream, this byte sequence will be added in its entirety, so as the compressor continues, it becomes more and more efficient; it approaches optimal compression.
At the end, the dictionary ends up containing:
| 256 | 'in' |
| 257 | 'n ' |
| 258 | ' t' |
| 259 | 'th' |
| 260 | 'he' |
| 261 | 'e ' |
| 262 | ' b' |
| 263 | 'be' |
| 264 | 'eg' |
| 265 | 'gi' |
| 266 | 'inn' |
| 267 | 'ni' |
| 268 | 'ing' |
| 269 | 'g ' |
| 270 | ' G' |
| 271 | 'Go' |
| 272 | 'od' |
| 273 | 'd ' |
| 274 | ' c' |
| 275 | 'cr' |
| 276 | 're' |
| 277 | 'ea' |
| 278 | 'at' |
| 279 | 'te' |
| 280 | 'ed' |
| 281 | 'd t' |
| 282 | 'the' |
| 283 | 'e h' |
| 284 | 'hea' |
| 285 | 'av' |
| 286 | 've' |
| 287 | 'en' |
| 288 | 'ns' |
| 289 | 's ' |
| 290 | ' a' |
| 291 | 'an' |
| 292 | 'nd' |
| 293 | 'd th' |
| 294 | 'he ' |
| 295 | ' e' |
| 296 | 'ear' |
| 297 | 'rt' |
| 298 | 'th.' |
69 6e 20 74 68 65 20 62 65 67 100 6e 101 67 20 47 6f 64 20 63 72 65 61 74 65 112 104 106 105 61 76 65 6e 73 20 61 6e 11a 105 20 116 72 104
This simple example doesn't make for a very impressive compression ratio; LZW doesn't perform well on short input. You can see as you work through the example, though, that the algorithm is starting to build up a more and more impressive dictionary. Given the entire book of genesis, LZW will achieve a better than 50% compression ratio. In general, the longer the source (and the greater its homogeneity), the better LZW performs.
Now, back to the question of the size of the dictionary. How big should the dictionary be? Well, at first, a new dictionary entry is created for each byte of the input stream. So, the dictionary will end up being on the order of the length of the input stream; however, as dictionary entries are matched, bytes are skipped over, so the dictionary won't grow quite so much as the document is scanned. To keep things efficient, LZW has us create a 512-entry dictionary until it fills up, and then double its size until it fills up again, and so on and so forth. This means that the compressor must emit 9 bit (log2512) codes until the dictionary fills up, and must then start emitting 10-bit codes, etc.
So, here's the code for the compression function:
void compress( const char *buf, int buflen )
{
char **dictionary;
int dictionary_ind;
int code;
int code_length = 9;
char *inp = buf;
// Create an initial dictionary with 2**9=512 entries. When this
// dictionary fills up, it will be expanded and the code size will
// increase.
dictionary = ( char ** ) malloc( sizeof( char * ) * ( 1 << code_length ) );
memset( dictionary, 0x0, sizeof( char * ) * ( 1 << code_length ) );
// pre-initialize the first 255 entries with their own values
for ( dictionary_ind = 0; dictionary_ind < 256; dictionary_ind++ )
{
dictionary[ dictionary_ind ] = ( char * ) malloc( 2 );
sprintf( dictionary[ dictionary_ind ], "%c", dictionary_ind );
}
// Compress until there's no more data
while ( buflen-- )
{
// Seach the dictionary for the longest match that matches
// inp
for ( i = dictionary_ind - 1; i; i-- )
{
if ( dictionary[ i ] != NULL )
{
if ( !strncmp( dictionary[ i ], inp,
strlen( dictionary[ i ] ) ) )
{
code = i;
break;
}
}
}
write_bits( code, out, code_length );
inp += strlen( dictionary[ code ] );
// Add this match, along with the next character, to the dictionary
dictionary[ dictionary_ind ] = malloc( strlen( dictionary[ code ] ) + 2 );
sprintf( dictionary[ dictionary_ind ], "%s%c", dictionary[ code ], *inp );
dictionary_ind++;
// Expand the dictionary if necessary
if ( dictionary_ind == ( 1 << code_length ) )
{
code_length++;
dictionary = realloc( dictionary,
sizeof( unsigned char ** ) * ( 1 << code_length ) );
}
}
}
Now... how does the decompressor decompress this, without access to the dictionary? It builds the same dictionary. It starts by initializing the first 255 entries, just as the compressor did, and then starts reading the compressed input. The first byte of compressed input is 0x69 (105), the ASCII code for 'i'. The decompressor does have an entry in its dictionary at index 105: the one-byte string 'i'. Moving on, it encounteres the code 0x6E (110), the ASCII code for 'n'. It outputs the value found at that entry in the dictionary (the one-byte string 'n'), and updates its own running dictionary with the previous two-byte sequence 'in'. When it gets to byte 10 of the compressed input, it encounters the code 256 - it consults its own running dictionary, finds the string 'in' and outputs that. Moving on, it finds the code 110, so it outputs dictionary[110] = 'n', and updates its own dictionary to contain the concatenation of this entry with the previous entry, getting dictionary[267] = 'inn'. As it reads each input code, the decompressor's dictionary matches the compressor's dictionary, so it can always find the correct data to output.
Here's the code for the decompressor:
int prev = -1;
int code;
int code_length = 9;
// Create a dictionary large enough to hold "code_length" entries.
// Once the dictionary overflows, code_length increases
dictionary = ( unsigned char ** ) malloc( sizeof( unsigned char * ) *
( 1 << code_length ) );
memset( dictionary, sizeof( unsigned char * ) * ( 1 << code_length ), 0x0 );
// Initialize the first 256 entries of the dictionary with their
// indices. The rest of the entries will be built up dynamically.
for ( dictionary_ind = 0; dictionary_ind < 256; dictionary_ind++ )
{
dictionary[ dictionary_ind ] = ( unsigned char * ) malloc( 2 );
sprintf( dictionary[ dictionary_ind ], "%c", dictionary_ind );
}
while ( ( code = read_next_code( code_length ) ) != -1 )
{
if ( prev > -1 )
{
dictionary[ dictionary_ind ] = ( unsigned char * ) malloc(
strlen( dictionary[ prev ] ) + 2 );
sprintf( dictionary[ dictionary_ind ], "%s%c", dictionary[ prev ],
dictionary[ code ][ 0 ] );
dictionary_ind++;
}
// Expand the dictionary if necessary
if ( dictionary_ind == ( 1 << code_length ) )
{
unsigned char **new_dictionary;
code_length++;
dictionary = ( unsigned char ** ) realloc( dictionary,
sizeof( unsigned char * ) * ( 1 << code_length ) );
}
prev = code;
}
This works — almost. As it turns out, this code will fail when it tries to decompress the compressed representation of:
aaaaaaaaaaaa
(12 a's) - or any other repeating sequence of a single byte. To see why, look at the behavior of the compression algorithm as it compresses this input. At step 1, the compressor is looking at:
aaaaaaaaaaaa ^
Searching through its dictionary, the longest match it finds is at position 97 (the entry for the single letter 'a'), so it outputs the code 97 and adds the entry 'aa' to its own dictionary at position 256. Now it advances by one and is looking at:
aaaaaaaaaaaa ^
Now it consults it dictionary and finds the longest match is at entry 256 — the entry that it just created! This isn't a problem for the encoder, but it is a problem for the decoder. The decoder receives the first code, 97, which it finds in its dictionary with no problem, and outputs the corresponding dictionary entry 'a'. It moves on to the next code and finds 256 — which isn't in its dictionary yet!
One brute-force solution to this problem would be to rigidly synchronize the encoder with the decoder. The encoder could delay adding entries to its dictionary by doing exactly what the decoder does; add an entry consisting of the previous match and the current character. The problem with this is that it would produce suboptimal results on repeating sequences like the sequence of 'a's above.
A more clever solution — and the one employed by actual LZW implementations — is to observe that this case only comes up when the encoder detects a match to an entry that it just added. This can only be the case when a previous dictionary entry is followed by its own first character in the input stream. Therefore, the decoder can safely infer that if it receives the "next code" before it's had a chance to read it, then this code must represent the previous match followed by its own first character.
Armed with this observation, you can modify the code in listing 3 to handle this case correctly:
if ( prev > -1 )
{
if ( code == dictionary_ind )
{
dictionary[ dictionary_ind ] = ( unsigned char * ) malloc(
strlen( dictionary[ prev ] ) + 2 );
sprintf( dictionary[ dictionary_ind ], "%s%c", dictionary[ prev ],
dictionary[ prev ][ 0 ] );
}
else
{
dictionary[ dictionary_ind ] = ( unsigned char * ) malloc(
strlen( dictionary[ prev ] ) + 2 );
sprintf( dictionary[ dictionary_ind ], "%s%c", dictionary[ prev ],
dictionary[ code ][ 0 ] );
dictionary_ind++;
}
}
Listing 4: Corrected uncompress code
Notice that only change between the two cases is that
dictionary[ code ] is not consulted, but instead
dictionary[ prev ] is.
The dictionary indices themselves are bigger than single bytes. How are these output onto a byte-delimited output stream? Since the purpose of LZW is to compress its input, it's necessary to pack these codes into bytes as efficiently as possible. Here's how the compressor outputs its codes one bit at a time onto a byte stream:
/**
* Write code_length bits of code (right-aligned) out to "out".
* Do so in little-endian order:
*
* 00100011 11010010 10111000 00011001
*
* 87654321 65432109 43210987 21098765
* 1111111 22222111 33322222
*/
static void write_bits( int code, int out, int code_length )
{
static unsigned char buf = 0x0;
static int bufpos = 0;
int mask_pos = 0;
while ( code_length-- )
{
buf |= ( ( code & ( 1 << mask_pos ) ) ? 1: 0 ) << bufpos;
mask_pos++;
if ( bufpos++ == 7 )
{
write( out, &buf, 1 );
buf = 0x0;
bufpos = 0;
}
}
}
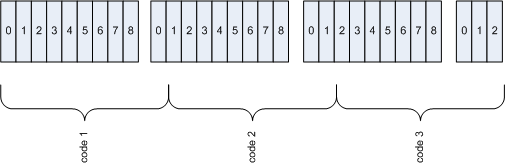
The choice of little-endian ordering here — where the bits are output in string least-significant-bit order — is somewhat arbitrary. This could just as legitimately have been implemented like this:
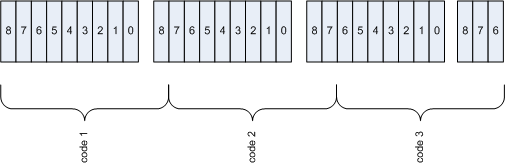
compress utility, even
though the codes are "backwards" (if you ask me).
Here's how the decompressor decodes these codes:
/**
* Given the input: 23 d2 b8 19, read in little-endian format:
*
* 00100011 11010010 10111000 00011001
*
* 87654321 65432109 43210987 21098765
* 1111111 22222111 33322222
*
* So the unpacked output is:
* (0 0010011) (00 1101001) (001 101110) (xxxx 00011)
*/
static int next_bit( int in )
{
static unsigned char byte;
static unsigned int mask = 0x100;
int bit;
if ( mask == 0x100 )
{
mask = 0x01;
if ( !read( in, &byte, 1 ) )
{
return -1;
}
}
bit = ( byte & mask ) ? 1 : 0;
mask << <= 1;
return bit;
}
int next_code( int code_length )
{
code = 0x0;
for ( i = 0; i < code_length; i++ )
{
int bit = next_bit( input );
if ( bit == -1 )
{
return -1;
}
code = code | ( bit << i );
}
return code;
}
You may have thought of a practical problem with the approach outlined so far, though. What happens if the document being compressed changes radically in the middle? Say, it switches from English to Spanish? Now the dictionary entries won't match — and you've already used up your dictionary entries. To guard against this possibility, LZW defines a special "clear code" that instructs the decompressor to discard its entire working dictionary, drop back to 9-bit codes, and essentially start over again in the middle of processing. It's up to the compressor to decide when or even if to send this clear code; robust compressors will ordinarily emit the clear code, and start the dictionary over, when very few matched (or mostly short matches) are detected during compression. The clear code itself is 256 - so the dictionary entry 256 is always NULL. (All of the previous examples in this article show entry 256 being used to store codes; real LZW implementations don't).
Another practical problem with the compressor code in listing 2 is that the entire buffer to be compressed has to be available in memory before compression can start. Since the point of compressing is to reduce the size of large files, it makes sense to extend this to buffer its input so that it can work on input files of arbitrary size. Although this isn't strictly related to the problem of compressing, it's made slightly more complicated by the compressor's requirement that it be able to scan forward through its buffer to an arbitrary length. This means that you can't just read the input stream a buffer at a time, but instead must implement a "sliding" buffer so that the remaining characters are always contiguous. A simple sliding buffer implementation (based on buffer swapping) is illustrated in listing 7:
buflen = read( in, buf, BUFSZ * 2 );
while ( inp < ( buf + buflen ) )
{
// Advance buffer
if ( ( inp - buf ) > BUFSZ )
{
memcpy( buf, inp, buflen - ( inp - buf ) );
buflen -= ( inp - buf );
buflen += read( in, buf + buflen, BUFSZ + ( BUFSZ - buflen ) );
inp = buf;
}
// Seach the dictionary for the longest match that matches
// inp
for ( i = dictionary_ind - 1; i; i-- )
{
Listing 7: Compressor with sliding window buffer
The code presented here is almost compatible with the standard Unix
compress utility. Although that utility is actually hard
to come by these days, there's a compatible uncompressor built into gzip.
However, gzip will not be able to operate on the output from listing 5
without a few more minor tweaks.
One obvious difference is that the compress utility outputs a standard header. It's not a very complex header, though - it's only three bytes long. The first two are the "magic" numbers 0x1f9d. The third byte is a descriptor byte. The most important part of this descriptor byte is the low-order 5 bits; the value of these five bits tell the decompressor the largest code in the data stream. This is important because, given a large volume of input, the implementation presented here will allow its codes to grow and grow without bounds. However, once you get to a certain point, expanding the dictionary further doesn't yield any meaningful compression, but it does use up memory as the dictionary gets larger and larger. The compressor is, therefore, allowed to say "there are no codes longer than 12 bits in this document; once you get to the end of the 12-bit code space, stop filling up the dictionary". Of course, the compressor might also emit a clear code after it fills up its 12-bit code space.
Here, then, is a complete code listing for a working LZW compressor.
#include <stdio.h>
#include <stdlib.h>
#include <errno.h>
#include <fcntl.h>
#include <string.h>
#define BUFSZ 256
/**
* Write code_length bits of code (right-aligned) out to "out".
* Do so in little-endian order:
*
* 00100011 11010010 10111000 00011001
*
* 87654321 65432109 43210987 21098765
* 1111111 22222111 33322222
*/
static void write_bits( int code, int out, int code_length )
{
static unsigned char buf = 0x0;
static int bufpos = 0;
int mask_pos = 0;
while ( code_length-- )
{
// right shift by bytes
buf |= ( ( code & ( 1 << mask_pos ) ) ? 1: 0 ) << bufpos;
mask_pos++;
if ( bufpos++ == 7 )
{
write( out, &buf, 1 );
buf = 0x0;
bufpos = 0;
}
}
}
int main( int argc, char *argv[ ] )
{
char buf[ BUFSZ * 2 ];
int buflen;
int in, out;
char *outfilename;
char **dictionary;
int dictionary_ind;
int code_length = 9;
int i;
int outc;
char *inp = buf;
int prev = -1;
if ( argc < 2 )
{
fprintf( stderr, "Usage: %s <file>\n", argv[ 0 ] );
exit( 0 );
}
if ( ( in = open( argv[ 1 ], O_RDONLY ) ) == -1 )
{
fprintf( stderr, "Unable to open input file '%s'", argv[ 1 ] );
perror( ": " );
exit( 0 );
}
outfilename = ( char * ) malloc( strlen( argv[ 1 ] ) + 3 );
sprintf( outfilename, "%s.Z", argv[ 1 ] );
if ( ( out = open( outfilename, O_WRONLY | O_CREAT | O_TRUNC, 0644 ) ) == -1 )
{
fprintf( stderr, "Unable to open output file '%s'", outfilename );
perror( ": " );
exit( 0 );
}
// Write out magic header 1f 9d
outc = 0x1f;
write( out, &outc, 1 );
outc = 0x9d;
write( out, &outc, 1 );
outc = 0x90; // bit 7 must be set for compatibility
write( out, &outc, 1 );
// Header done; start compressing
// Create an initial dictionary with 2**9=512 entries. When this
// dictionary fills up, it will be expanded and the code size will
// increase.
dictionary = ( char ** ) malloc( sizeof( char * ) * ( 1 << code_length ) );
memset( dictionary, 0x0, sizeof( char * ) * ( 1 << code_length ) );
// pre-initialize the first 255 entries with their own values
for ( dictionary_ind = 0; dictionary_ind < 256; dictionary_ind++ )
{
dictionary[ dictionary_ind ] = ( char * ) malloc( 2 );
sprintf( dictionary[ dictionary_ind ], "%c", dictionary_ind );
}
// Skip 256 (this is the clear code)
dictionary_ind++;
buflen = read( in, buf, BUFSZ * 2 );
while ( inp <= ( buf + buflen ) )
{
// Advance buffer
if ( ( inp - buf ) > BUFSZ )
{
memcpy( buf, inp, buflen - ( inp - buf ) );
buflen -= ( inp - buf );
buflen += read( in, buf + buflen, BUFSZ + ( BUFSZ - buflen ) );
inp = buf;
}
// Seach the dictionary for the longest match that matches
// inp
for ( i = dictionary_ind - 1; i; i-- )
{
if ( dictionary[ i ] != NULL )
{
if ( !strncmp( dictionary[ i ], inp,
strlen( dictionary[ i ] ) ) )
{
outc = i;
break;
}
}
}
write_bits( outc, out, code_length );
inp += strlen( dictionary[ outc ] );
// Add this match, along with the next character, to the dictionary
dictionary[ dictionary_ind ] = malloc( strlen( dictionary[ outc ] ) + 2 );
sprintf( dictionary[ dictionary_ind ], "%s%c", dictionary[ outc ], *inp );
dictionary_ind++;
// Expand the dictionary if necessary
if ( dictionary_ind == ( 1 << code_length ) )
{
code_length++;
dictionary = realloc( dictionary,
sizeof( unsigned char ** ) * ( 1 << code_length ) );
}
}
}
Listing 8: Complete compressor code
Also, although it seems nitpicky (and it is!), if you use the compressor
presented here, it still won't work correctly with a proper
uncompress implementation. Why? Well, when the dictionary
goes from 511 to 512 entries, the code length goes from 9 to 10 bits. However,
its impossible for the very next code that's emitted to be a 10 bit code.
so, in order to wring every last drop of compression out of the implementation,
compress doesn't start emitting 10-bit codes until the next
entry (that single bit matters!). Therefore, in order to maintain
compatibility with the de facto standard, you'll need to modify listing 8
slightly:
write_bits( outc, out, code_length );
inp += strlen( dictionary[ outc ] );
// Expand the dictionary if necessary
if ( dictionary_ind == ( 1 << code_length ) )
{
code_length++;
dictionary = realloc( dictionary,
sizeof( unsigned char ** ) * ( 1 << code_length ) );
}
// Add this match, along with the next character, to the dictionary
dictionary[ dictionary_ind ] = malloc( strlen( dictionary[ outc ] ) + 2 );
sprintf( dictionary[ dictionary_ind ], "%s%c", dictionary[ outc ], *inp );
dictionary_ind++;
}
}
Listing 9: Compressor code compatible with uncompress
The complete decompressor is shown in listing 10:
#include <stdio.h>
#include <stdlib.h>
#include <errno.h>
#include <fcntl.h>
#include <string.h>
/**
* Given the input: 23 d2 b8 19, read in little-endian format:
*
* 00100011 11010010 10111000 00011001
*
* 87654321 65432109 43210987 21098765
* 1111111 22222111 33322222
*
* So the unpacked output is:
* (0 0010011) (00 1101001) (001 101110) (xxxx 00011)
*/
static int next_bit( int in )
{
static unsigned char byte;
static unsigned int mask = 0x100;
int bit;
if ( mask == 0x100 )
{
mask = 0x01;
if ( !read( in, &byte, 1 ) )
{
return -1;
}
}
bit = ( byte & mask ) ? 1 : 0;
mask <<= 1;
return bit;
}
int main( int argc, char *argv[] )
{
int input;
int maxbits;
int code_length = 9;
int i;
unsigned char magic[ 2 ];
unsigned char header;
int code, prev = -1;
unsigned char **dictionary;
int dictionary_ind;
if ( argc < 2 )
{
fprintf( stderr, "Usage: %s <input file>\n", argv[ 0 ] );
exit( 0 );
}
input = open( argv[ 1 ], O_RDONLY );
if ( input == -1 )
{
fprintf( stderr, "Error opening file '%s'", argv[ 1 ] );
perror( ":" );
}
// LZW starts with two bytes of "magic"
read( input, &magic, 2 );
if ( ( magic[ 0 ] != 0x1f ) ||
( magic[ 1 ] != 0x9d ) )
{
fprintf( stderr, "This is not a compressed file." );
exit( 0 );
}
// followed by a single byte of header info
read( input, &header, 1 );
maxbits = header & 0x1f;
// Create a dictionary large enough to hold "code_length" entries.
// Once the dictionary overflows, code_length increases
dictionary = ( unsigned char ** ) malloc( sizeof( unsigned char * ) *
( 1 << code_length ) );
memset( dictionary, sizeof( unsigned char * ) * ( 1 << code_length ), 0x0 );
// Initialize the first 256 entries of the dictionary with their
// indices. The rest of the entries will be built up dynamically.
for ( dictionary_ind = 0; dictionary_ind < 256; dictionary_ind++ )
{
dictionary[ dictionary_ind ] = ( unsigned char * ) malloc( 2 );
sprintf( dictionary[ dictionary_ind ], "%c", dictionary_ind );
}
// 256 is the special "clear" code; don't give it an entry here
dictionary_ind++;
// followed by the compressed data itself. Read the data 9 bits
// at a time. .Z formatted data always starts with 9 bit codes.
{
int done = 0;
while ( !done )
{
code = 0x0;
for ( i = 0; i < code_length; i++ )
{
int bit = next_bit( input );
if ( bit == -1 )
{
done = 1;
break;
}
code = code | ( bit << i );
}
if ( code == 256 )
{
code_length = 9;
dictionary = ( unsigned char ** ) realloc( dictionary,
sizeof( unsigned char * ) * ( 1 << code_length ) );
}
// Update the dictionary with this character plus the _entry_
// (character or string) that came before it
if ( prev > -1 )
{
if ( code == dictionary_ind )
{
dictionary[ dictionary_ind ] = ( unsigned char * ) malloc(
strlen( dictionary[ prev ] ) + 2 );
sprintf( dictionary[ dictionary_ind ], "%s%c", dictionary[ prev ],
dictionary[ prev ][ 0 ] );
}
else
{
dictionary[ dictionary_ind ] = ( unsigned char * ) malloc(
strlen( dictionary[ prev ] ) + 2 );
sprintf( dictionary[ dictionary_ind ], "%s%c", dictionary[ prev ],
dictionary[ code ][ 0 ] );
}
dictionary_ind++;
if ( dictionary_ind == ( 1 << code_length ) )
{
unsigned char **new_dictionary;
//printf( "End of dictionary.\n" );
code_length++;
dictionary = ( unsigned char ** ) realloc( dictionary,
sizeof( unsigned char * ) * ( 1 << code_length ) );
}
}
if ( dictionary[ code ] == NULL )
{
printf( "Error in dictionary (no entry for code %d).\n", code );
exit( 0 );
}
printf( "%s", dictionary[ code ] );
prev = code;
}
}
printf( "\n" );
close( input );
}
Listing 10: Complete decompressor
There are some obvious performance improvements you can make over the code presented here. For example, the dictionary implementation here grows and grows, repeating itself quite a bit. Real LZW implementations put a bound on the size of each dictionary entry by implementing the dictionary as a smarter data structure that consists of the last byte of the string, followed by a "back pointer" to the previous byte of the string. Further, in this simple implementation, I'm performing a linear search over the entire dictionary for each input byte. However, if the input byte is 'a', there's no reason to search the strings that start with 'b'. Therefore, optimal implementations employ more sophisticated data structures to speed up the match search function.
Another problem is that this code will only work on text data - since I'm using the strcmp and strlen functions to do dictionary matching, embedded NULLs will cause this to fail. I'll fix both of these problems in a future installment of this series, and illustrate how to turn this code into a functioning GIF decoder.
References:
- Jacob Ziv and Abraham Lempel "A Universal Algorithm for Sequential Data Compression", IEEE Transactions on Information Theory, 23(3), pp. 337-343, May 1977
- Jacob Ziv and Abraham Lempel "Compression of Individual Sequences via Variable-Rate Coding", IEEE Transactions on Information Theory, 24(5), pp. 530-536, September 1978
- Terry Welch "A Technique for High-Performance Data Compression", IEEE Computer, June 1984
Add a comment:
Completely off-topic or spam comments will be removed at the discretion of the moderator.
You may preserve formatting (e.g. a code sample) by indenting with four spaces preceding the formatted line(s)
thank you
(i) shouldn't dictionary_ind be reset to 257?
(ii) shouldn't the code 'continue' to read the next code instead of processing clear code?00100011 11010010 10111000 00011001then, omitting the header bytes, I end up with
00100011 10100100 11100001 11001010 00000000What does the tool do differently?


The first two character entry in the dictionary is "in" and thus has a hex index of 100, but in the example lzw sequence the value presented is 101.
Note to moderator: it's completely ok to delete my comments here if you change the text so that these are no longer issues (or if I am somehow wrong, of course).