How Certificates Use Digital Signatures
Anybody who's been using the web for any appreciable amount of time has been presented with ominous, but vague, security warnings such as "this site's certificate has expired", "this site was signed by an untrusted certificate authority", or "the domain name in this site's certificate doesn't match the domain name you've connected to." Research has borne out that most people ignore these warning messages when they're browsing - and honestly, how many of us really know how worried to be? Many web users — even experienced ones — have only a vague notion of what a "certificate" is and what it's for. However, the concept of a certificate — more accurately, an X.509 certificate [1] — is central to modern software security.
As you can probably guess, web browsers secure their traffic using digital
cryptography algorithms. Digital cryptography algorithms are "key-based" -
meaning that sensitive input is obscured by applying a mathematical algorithm
to the input along with a secret key in order to produce meaningless
gibberish — gibberish, at least, to everybody except a holder of the
secret key. In mathematical terminology, an encryption algorithm
E is applied to the sensitive plaintext P
along with a secret key K to produce the ciphertext
C which can be safely transmitted over an open channel. More
succinctly, C = E(P,K). Similarly, a decryption algorithm D is
applied by the recipient to retrieve the original plaintext:
P = D(C,K).
Broadly speaking, there are two categories of digital cryptography algorithms — symmetric and public. In symmetric algorithms, the same key is used to decrypt the encrypted data as was used to encrypt it in the first place. In public algorithms, the key itself is split into two pieces. One piece is used to encrypt, and the other piece is used to decrypt. The two keys are tightly related — actually generating a public/private keypair is a tricky and precise operation — but once generated, the public key can be freely, and safely, distributed.
The public key is used to do the encrypting, and the private key is used to do the decrypting. This allows two parties to exchange information over a plaintext, unsecured channel without ever meeting or exchanging secrets out of band. The recipient can generate a keypair, send the public key over the insecure channel, and wait for the sender to encrypt something using it. At this point, only the recipient — the holder of the private key — can decrypt the data.
Although there are a few different public-key encryption algorithms, the most
popular — and fortunately, the easiest to understand — is the
RSA algorithm, named after its three inventors Rivest, Shamir and Adelman.
To apply the RSA algorithm, you must find three numbers e,
d and n related such that
((me)d) % n = m.
Here, e and n comprise the public key and
d is the private key. When one party wishes to send a message
in confidence to the holder of the private key, he computes and transmits
c = (me) % n. The recipient
then recovers the original message m using
m = (cd) % n.
This almost works. There's a flaw, though, called the "man-in-the- middle" attack. It works like this: an eavesdropper situates himself in between the sender and the recipient. When the would-be recipient transmits his public key, the eavesdropper intercepts it and replaces it with his own public key. The sender, none the wiser, uses this fake public key to encrypt his data. The eavesdropper decrypts it using his own private key, re-encrypts using the recipients public key, and sends it on its way. Neither the sender nor the receiver can detect this, and the whole point of using encryption has been defeated - any sufficiently motivated attacker can listen in on any seemingly secure conversation.
The best known solution to this problem is what's referred to as a "public key infrastructure" (PKI). At the heart of a PKI is a set of trusted authorities who can vouch for the validity of a public key. In this way, if you get a public key from Bob, you just need to check with the trusted authority whether or not this is really Bob's public key. If it's been replaced by a man in the middle, the authority will detect this and warn you.
All well and good, but how do you establish the trust relationship with the authorities in the first place? How do you know that you're talking to an authority and not yet another man-in-the-middle? The answer, again, is centered around public keys — but this time, the purposes are reversed. Just as a public key can be used to encrypt data for the entity that holds the private key, a private key can be used to prove ownership of a public key. Instead of the sender encrypting the data with the public key, the asserting party (the one with the private key) encrypts a bit of data with the private key, and sends both that data (in the clear) and the encrypted data itself. As it turns out, public-key cryptography works in such a way that only the holder of the private key can do this - so if you have access to the public key, you can use it to decrypt the data. If it matches the "token" data, then you can be assured that it was generated by the holder of the private key. Such a token/encrypted data pair is called a digital signature. This works, conceptually at least, like a handwritten signature. Only one person can generate such a handwritten signature (we hope), and that person is assumed to have read over the paper that he's signing. He signs it in ink so that it becomes part of the document, and a future third party can verify the signature to assert that the document was written (or at least authorized) by the signer.
When a keypair is used to sign a message this way, rather than computing
c = me%n, the signature is computed as
s = md%n (remember that d is the private
key, not shared with anybody else). The recipient, who has the public key,
can verify the signature by verifying that m = se%n.
If so, then s could only have been generated by the holder of the
private key. One practical problem with this approach is that s
would end up being very long (as long as m), so a cryptographically
secure hash such as MD5 or SHA-1[2] which was generated uniquely from m
is typically used instead.
This approach allows one party to "vouch" for another. One trusted party can sign the public key of another; the recipient can check the signature and, if he trusts the signer, can be assured that the public key belongs to the bearer. In modern PKI terminology, such a trusted signing party is referred to as a certificate authority. Of course, for this to work, a trust relationship must be established with the certificate authority out of band, but only needs to be done once — once this is done, all subsequent public keys can be checked dynamically.
So, what does all this have to do with certificates? Well, fundamentally, a certificate is a holder for public key, along with a few assertions about the owner of the public key. When you establish a secure connection with a website, that website presents a certificate containing, at least, two pieces of information: the public key of the site and the digital signature supplied by a trusted certificate authority. The browser then uses that public key to establish a secure connection.
Take a look at Amazon's SSL certificate.
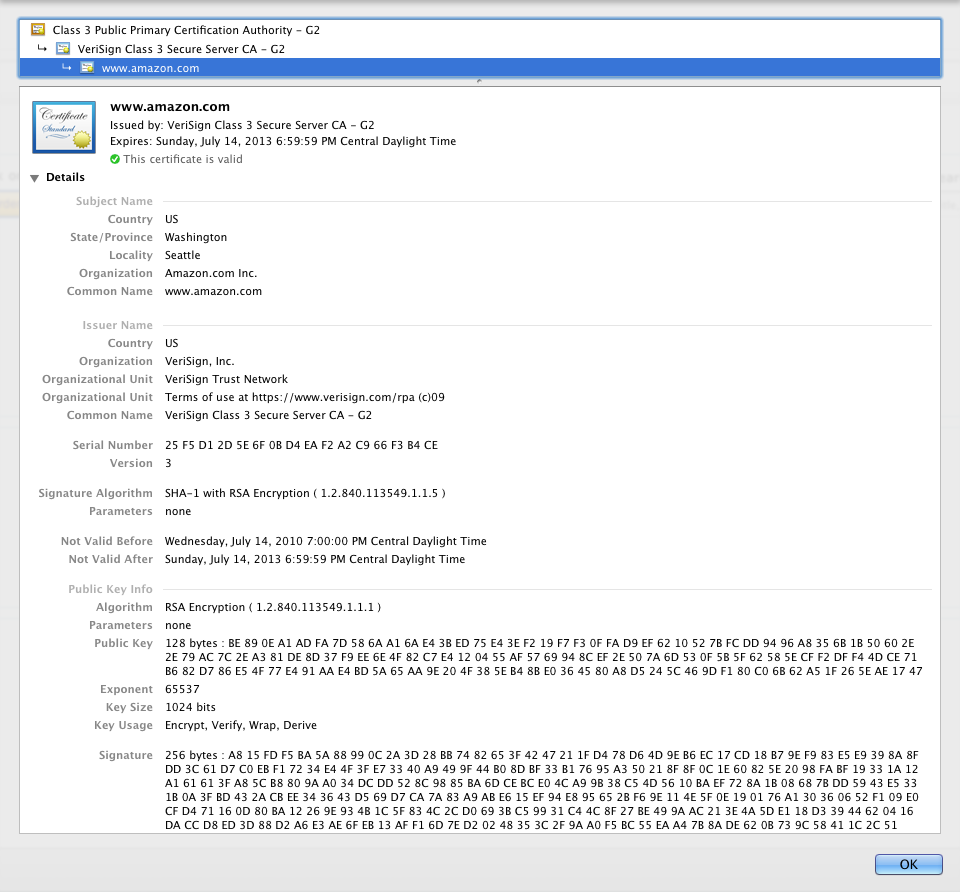
Figure 1: Amazon's SSL Certificate
You can see this yourself if you navigate to a secured page on Amazon.com (for instance, your account page), and click the "lock" icon on your browser.
Openssl can output the full details of a certificate in a convenient format:
$ openssl x509 -text -noout -in amazon.cer
Certificate:
Data:
Version: 3 (0x2)
Serial Number:
25:f5:d1:2d:5e:6f:0b:d4:ea:f2:a2:c9:66:f3:b4:ce
Signature Algorithm: sha1WithRSAEncryption
Issuer: C=US, O=VeriSign, Inc., OU=VeriSign Trust Network,
OU=Terms of use at https://www.verisign.com/rpa (c)09,
CN=VeriSign Class 3 Secure Server CA - G2
Validity
Not Before: Jul 15 00:00:00 2010 GMT
Not After : Jul 14 23:59:59 2013 GMT
Subject: C=US, ST=Washington, L=Seattle, O=Amazon.com Inc.,
CN=www.amazon.com
Subject Public Key Info:
Public Key Algorithm: rsaEncryption
RSA Public Key: (1024 bit)
Modulus (1024 bit):
00:be:89:0e:a1:ad:fa:7d:58:6a:a1:6a:e4:3b:ed:
75:e4:3e:f2:19:f7:f3:0f:fa:d9:ef:62:10:52:7b:
fc:dd:94:96:a8:35:6b:1b:50:60:2e:2e:79:ac:7c:
2e:a3:81:de:8d:37:f9:ee:6e:4f:82:c7:e4:12:04:
55:af:57:69:94:8c:ef:2e:50:7a:6d:53:0f:5b:5f:
62:58:5e:cf:f2:df:f4:4d:ce:71:b6:82:d7:86:e5:
4f:77:e4:91:aa:e4:bd:5a:65:aa:9e:20:4f:38:5e:
b4:8b:e0:36:45:80:a8:d5:24:5c:46:9d:f1:80:c0:
6b:62:a5:1f:26:5e:ae:17:47
Exponent: 65537 (0x10001)
X509v3 extensions:
X509v3 Basic Constraints:
CA:FALSE
X509v3 Key Usage:
Digital Signature, Key Encipherment
X509v3 CRL Distribution Points:
URI:http://SVRSecure-G2-crl.verisign.com/SVRSecureG2.crl
X509v3 Certificate Policies:
Policy: 2.16.840.1.113733.1.7.23.3
CPS: https://www.verisign.com/rpa
X509v3 Extended Key Usage:
TLS Web Server Authentication, TLS Web Client Authentication
X509v3 Authority Key Identifier:
keyid:A5:EF:0B:11:CE:C0:41:03:A3:4A:65:90:48:
B2:1C:E0:57:2D:7D:47
Authority Information Access:
OCSP - URI:http://ocsp.verisign.com
CA Issuers -
URI:http://SVRSecure-G2-aia.verisign.com/SVRSecureG2.cer
1.3.6.1.5.5.7.1.12:
0`.^.\0Z0X0V..image/gif0!0.0...+......Kk.(.....R8.).K..!..0
&.$http://logo.verisign.com/vslogo1.gif
Signature Algorithm: sha1WithRSAEncryption
a8:15:fd:f5:ba:5a:88:99:0c:2a:3d:28:bb:74:82:65:3f:42:
47:21:1f:d4:78:d6:4d:9e:b6:ec:17:cd:18:b7:9e:f9:83:e5:
e9:39:8a:8f:dd:3c:61:d7:c0:eb:f1:72:34:e4:4f:3f:e7:33:
40:a9:49:9f:44:b0:8d:bf:33:b1:76:95:a3:50:21:8f:8f:0c:
1e:60:82:5e:20:98:fa:bf:19:33:1a:12:a1:61:61:3f:a8:5c:
b8:80:9a:a0:34:dc:dd:52:8c:98:85:ba:6d:ce:bc:e0:4c:a9:
9b:38:c5:4d:56:10:ba:ef:72:8a:1b:08:68:7b:dd:59:43:e5:
33:1b:0a:3f:bd:43:2a:cb:ee:34:36:43:d5:69:d7:ca:7a:83:
a9:ab:e6:15:ef:94:e8:95:65:2b:f6:9e:11:4e:5f:0e:19:01:
76:a1:30:36:06:52:f1:09:e0:cf:d4:71:16:0d:80:ba:12:26:
9e:93:4b:1c:5f:83:4c:2c:d0:69:3b:c5:99:31:c4:4c:8f:27:
be:49:9a:ac:21:3e:4a:5d:e1:18:d3:39:44:62:04:16:da:cc:
d8:ed:3d:88:d2:a6:e3:ae:6f:eb:13:af:f1:6d:7e:d2:02:48:
35:3c:2f:9a:a0:f5:bc:55:ea:a4:7b:8a:de:62:0b:73:9c:58:
41:1c:2c:51
Toward the top, underneath "Data", you can see the "Subject" of "C=US,
ST=Washington, L=Seattle, O=Amazon.com Inc., CN=www.amazon.com". This
is telling you who the certificate is asserting is identified by the public
key. The most important part of the subject name is the "common name" (CN) - here
listed as www.amazon.com. This must match the DNS name of the website
that you're connecting to, or your browser will alert you that the certificate
is associated with a different domain than the one it was expecting. This
makes sense - this is what stops somebody from grabbing Amazon's certificate
and masquerading as Amazon on a site named www.scammer.com.
Below the subject name, you'll see the public key itself. The
algorithm is RSA. The exponent e is 65537 and the modulus
n is a 128-byte behemoth. What you see here is the hexadecimal representation of a 1,024-bit number. There's no further encoding here;
this is the number n used by the RSA algorithm. Notice that it's
prefixed by a 0x00 placeholder — this is used to stop some large-number
libraries from interpreting this as a negative two's-complement number.
If your browser decides to accept this certificate (see below), it
will generate yet another key — a one-time-use symmetric cryptography
key and securely transmit it to Amazon using the RSA algorithm
c=ke%n. Amazon will decrypt it using the private key
(which you can't see in the certificate for obvious reasons!) and
use that key for subsequent communications.
Just above the subject is the Issuer. This indicates who the signer of this certificate is — in other words, what entity is vouching that this public key does really identify www.amazon.com. After all, anybody could generate a keypair and a certificate that includes a common name of "www.amazon.com". Here, the trusted issuer is identified as "Verisign Class 3 Secure Server CA - G2". The whole thing is signed by "Verisign Class 3 Secure Server CA - G2"'s private key and the signature is shown at the very bottom (and is even longer than the public key modulus!)
So, before accepting this certificate as fact and establishing a secure
link with this server, your browser must verify that the signature was generated
by "Verisign Class 3 Secure Server CA - G2". First, it computes the secure
hash of the whole certificate using the identified signature algorithm "SHA-1".
Then it takes the signature and computes se'%n' where
e' and n' are the issuer's public key (I'll
show you an example in just a minute). It
compares this with the hash that it computed — if they match, the
certificate is valid (or, at least, it was really signed by Verisign Class
3 Secure Server CA - G2).
What you don't see in this certificate, though, is e' and
n' themselves. This makes sense - these numbers have to come
from somewhere else, or this certificate would be "self-identifying", which
is exactly the problem we're trying to avoid. In fact, the server gave me
another certificate - the one containing the signing key.
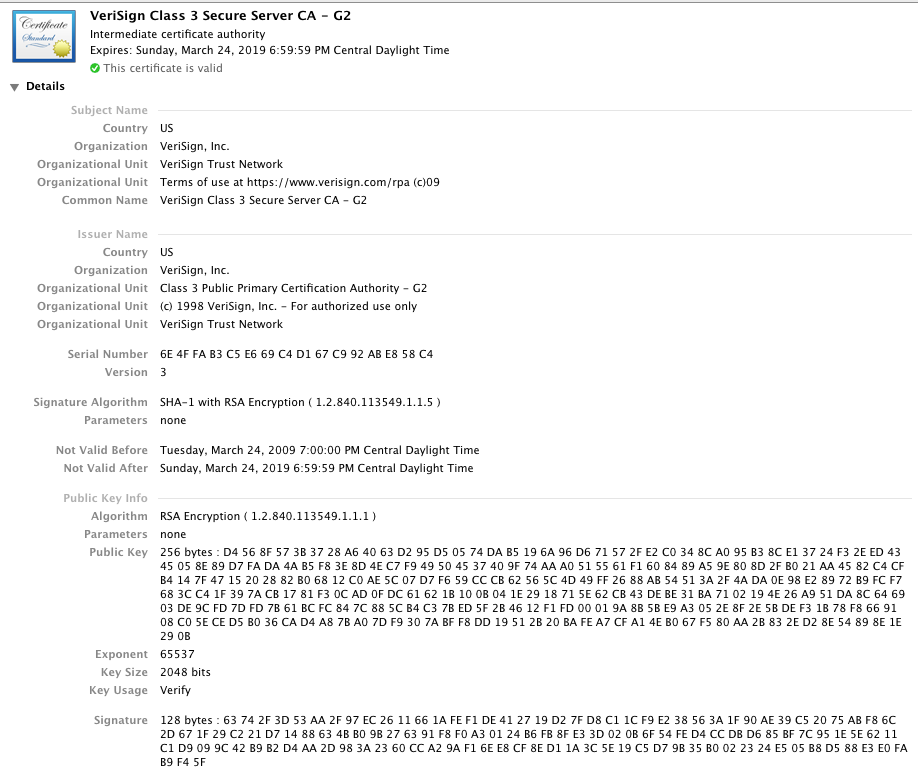
Figure 2: Verisign Class 3 Secure server CA - G2
Notice that the subject name matches, element for element, the issuer name of the previous certificate. This certificate has its own issuer, public key, and signature, just like the previous certificate as well. And the certificate associated with that signature is displayed:
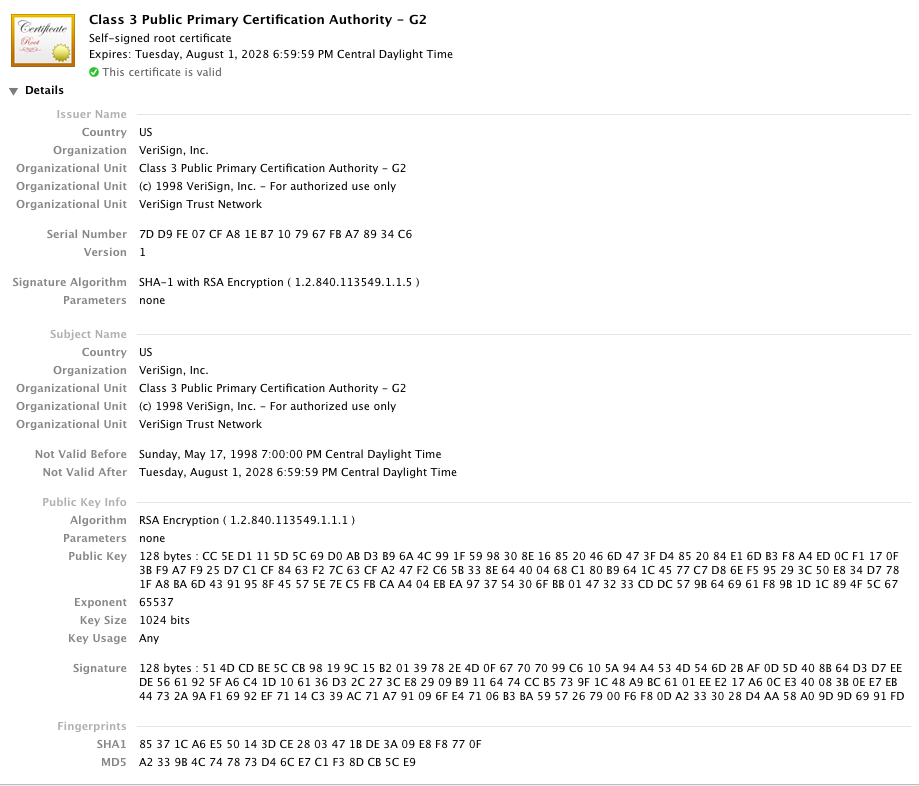
Figure 3: Verisign Trust Network
Now this is interesting - this certificate lists the same entity in the issuer as in the subject. This certificate is said to be "self-signed" — you can use the public key in the certificate to verify the signature. This is also the same public key that's used to verify the signature of the previous certificate. There are no higher-level certificates — the certificate "chain" ends here.
So far, although the process was complicated, it doesn't seem to have accomplished much — it wouldn't be that hard for an unscrupulous website to generate three fraudulent certificates which vouched for each other, ending in a self-signed top-level certificate. The final piece of the puzzle that holds this whole scheme together is a list of implicitly trusted certificates. Your browser comes with a list of (quite a few) implicitly trusted root certificates — one of these is the certificate in figure 3.
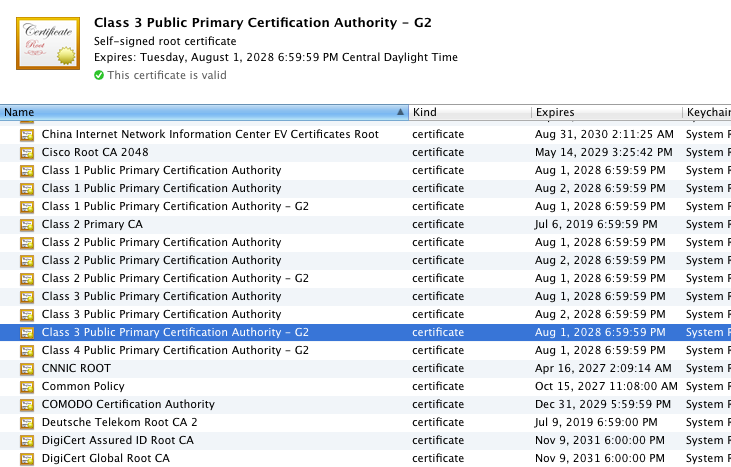
Figure 4: Trusted Roots
In fact, Amazon didn't actually send this certificate — they only sent me the first two, leaving it up to my browser to find the third, top-level certificate to complete the verification process. I can verify this by opening up wireshark and looking at the server certificate message.
Since my browser implicitly trusts this certificate, it permits it to sign the intermediate certificate in figure 2 which it then in turn permits to sign the server certificate in figure 1, and the public key is accepted as belonging to www.amazon.com. The value in the root certificates lies in your belief that they spent some time verifying that the entity who requested that they sign this certificate really represented the website identified in the common name. I can tell you from experience that this validation varies greatly from one CA to the next. Verisign has refused to issue certificates to me because the articles of incorporation my company filed with the U.S. government didn't match the domain name (!), but GoDaddy just checks to see if they can e-mail the owner of the site as listed by DNS.
It's interesting, and illustrative, to go through the verification process manually (of course, normally, your browser will do it for you automatically so you don't have to). The top-level certificate's public key (the modulus) is the 128-byte value:
CC5ED1115D5C69D0ABD3B96A4C991F5998308E168520466D473FD4852084E16DB3F8A4ED0C F1170F3BF9A7F925D7C1CF8463F27C63CFA247F2C65B338E64400468C180B9641C4577C7D8 6EF595293C50E834D7781FA8BA6D4391958F45575E7EC5FBCAA404EBEA973754306FBB0147 3233CDDC579B646961F89B1D1C894F5C67According to the RSA signature algorithm, this means that its own (self- signed) signature value of:
514DCDBE5CCB98199C15B20139782E4D0F67707099C6105A94A4534D546D2BAF0D5D408B64 D3D7EEDE5661925FA6C41D106136D32C273CE82909B9116474CCB5739F1C48A9BC6101EEE2 17A60CE340083B0EE7EB44732A9AF16992EF7114C339AC71A791096FE47106B3BA59572679 00F6F80DA2333028D4AA58A09D9D6991FDif raised to the power of the exponent 65537 and then divided by the modulus, should yield a remainder of the SHA-1 hash of:
D95944F5BD92127092218F9F02C719C42386B499(This is, incidentally, not the fingerprint of the certificate displayed in the certificate details window - that fingerprint is generated from the whole certificate, including the signature itself. The signature, obviously, doesn't include itself). This isn't the sort of computation you'd probably want to undertake using pencil and paper (although you're more than welcome to try if you'd like). It's easier to use, for example, Python:
>>> modulus = 0xCC5ED1115D5C69D0ABD3B96A4C991F5998308E168520466D473FD48520 84E16DB3F8A4ED0CF1170F3BF9A7F925D7C1CF8463F27C63CFA247F2C65B338E64400468C1 80B9641C4577C7D86EF595293C50E834D7781FA8BA6D4391958F45575E7EC5FBCAA404EBEA 973754306FBB01473233CDDC579B646961F89B1D1C894F5C67 >>> signature = 0x514DCDBE5CCB98199C15B20139782E4D0F67707099C6105A94A4534D 546D2BAF0D5D408B64D3D7EEDE5661925FA6C41D106136D32C273CE82909B9116474CCB573 9F1C48A9BC6101EEE217A60CE340083B0EE7EB44732A9AF16992EF7114C339AC71A791096F E47106B3BA5957267900F6F80DA2333028D4AA58A09D9D6991FD >>> print "%x" % pow( signature, 65537, modulus ) 1fffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff fffffffffffffffffffffffffffffffff003021300906052b0e03021a05000414d95944f5b d92127092218f9f02c719c42386b499The first bit, the 1fff... part, is the standard RSA algorithm padding and can be removed (if not present, the signature isn't checked any further). What remains is an ASN.1 encoding of the HMAC value. I won't go into the details of ASN.1 parsing here, but the important part is the hash code at the end: D95944F5BD92127092218F9F02C719C42386B499. (The part at the beginning declares both the length and the type — SHA-1 — of the hash code).
Note that this SHA-1 hash is not, itself, stored with the certificate; it's computed by running the contents of the certificate, minus the signature itself, through the SHA-1 algorithm. This way, any change in the certificate body will be detected immediately - the SHA-1 hash won't match the one in the signature.
Now, according to the rules of PKI, the second-level certificate's signature value of:
63742F3D53AA2F97EC2611661AFEF1DE412719D27FD8C11CF9E238563A1F90AE39C52075AB F86C2D671F29C221D71488634BB09B276391F8F0A30124B6FB8FE33D020B6F54FED4CCDBD6 85BF7C951E5E6211C1D9099C42B9B2D4AA2D983A2360CCA29AF16EE8CF8ED11A3C5E19C5D7 9B35B0022324E505B8D588E3E0FAB9F45Fif "decrypted" using the public key of the top-level certificate, should yield its SHA-1 signature of
08D1DEAF89D0976A5EE8E32DF210C415F6FC8571Again, this can be verified using Python:
>>> modulus = 0xCC5ED1115D5C69D0ABD3B96A4C991F5998308E168520466D473FD48520 84E16DB3F8A4ED0CF1170F3BF9A7F925D7C1CF8463F27C63CFA247F2C65B338E64400468C1 80B9641C4577C7D86EF595293C50E834D7781FA8BA6D4391958F45575E7EC5FBCAA404EBEA 973754306FBB01473233CDDC579B646961F89B1D1C894F5C67 >>> signature = 0x63742F3D53AA2F97EC2611661AFEF1DE412719D27FD8C11CF9E23856 3A1F90AE39C52075ABF86C2D671F29C221D71488634BB09B276391F8F0A30124B6FB8FE33D 020B6F54FED4CCDBD685BF7C951E5E6211C1D9099C42B9B2D4AA2D983A2360CCA29AF16EE8 CF8ED11A3C5E19C5D79B35B0022324E505B8D588E3E0FAB9F45F >>> print "%x" % pow( signature, 65537, modulus ) 1fffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff fffffffffffffffffffffffffffffffff003021300906052b0e03021a0500041408d1deaf8 9d0976a5ee8e32df210c415f6fc8571
This establishes that the public key in the intermediate certificate can be trusted as belonging to the entity named "VeriSign Class 3 Secure Server CA - G2". Now that this has been established, the browser goes on to check whether the signature in the bottom-level (Amazon's) certificate is valid. Again, this means that the certificate's SHA-1 hash value of:
B8F567ABED956D58069C95B644C702537D22EB86must be the RSA-encrypted value of the signature:
A815FDF5BA5A88990C2A3D28BB7482653F4247211FD478D64D9EB6EC17CD18B79EF983E5E9 398A8FDD3C61D7C0EBF17234E44F3FE73340A9499F44B08DBF33B17695A350218F8F0C1E60 825E2098FABF19331A12A161613FA85CB8809AA034DCDD528C9885BA6DCEBCE04CA99B38C5 4D5610BAEF728A1B08687BDD5943E5331B0A3FBD432ACBEE343643D569D7CA7A83A9ABE615 EF94E895652BF69E114E5F0E190176A130360652F109E0CFD471160D80BA12269E934B1C5F 834C2CD0693BC59931C44C8F27BE499AAC213E4A5DE118D33944620416DACCD8ED3D88D2A6 E3AE6FEB13AFF16D7ED20248353C2F9AA0F5BC55EAA47B8ADE620B739C58411C2C51As encrypted using the issuer's public key modulus. Again, you can use Python to verify that this is the case:
>>> signature = 0xa815fdf5ba5a88990c2a3d28bb7482653f4247211fd478d64d9eb6ec 17cd18b79ef983e5e9398a8fdd3c61d7c0ebf17234e44f3fe73340a9499f44b08dbf33b176 95a350218f8f0c1e60825e2098fabf19331a12a161613fa85cb8809aa034dcdd528c9885ba 6dcebce04ca99b38c54d5610baef728a1b08687bdd5943e5331b0a3fbd432acbee343643d5 69d7ca7a83a9abe615ef94e895652bf69e114e5f0e190176a130360652f109e0cfd471160d 80ba12269e934b1c5f834c2cd0693bc59931c44c8f27be499aac213e4a5de118d339446204 16daccd8ed3d88d2a6e3ae6feb13aff16d7ed20248353c2f9aa0f5bc55eaa47b8ade620b73 9c58411c2c51 >>> modulus = 0xd4568f573b3728a64063d295d50574dab5196a96d671572fe2c0348ca0 95b38ce13724f32eed4345058e89d7fada4ab5f83e8d4ec7f949504537409f74aaa0515561 f1608489a59e808d2fb021aa4582c4cfb4147f4715202882b06812c0ae5c07d7f659cccb62 565c4d49ff2688ab54513a2f4ada0e98e28972b9fcf7683cc41f397acb1781f30cad0fdc61 621b100b041e2918715e62cb43debe31ba7102194e26a951da8c646903de9cfd7dfd7b61bc fc847c885cb4c37bed5f2b4612f1fd00019a8b5be9a3052e8f2e5bdef31b78f8669108c05e ced5b036cad4a87ba07df9307abff8dd19512b20bafea7cfa14eb067f580aa2b832ed28e54 898e1e290b >>> print "%x" % pow( signature, 65537, modulus ) 1fffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff fffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff0030213 00906052b0e03021a05000414b8f567abed956d58069c95b644c702537d22eb86
Now, if I trust the issuer of this certificate, which I do because I trust the issuer of that certificate, which I do because Chrome (my browser) told me it was safe to, I can implicitly trust all of the information contained in the certificate. In particular, I can trust that the server that hosts www.amazon.com contains the private key corresponding to the public key contained in the presented certificate. Therefore, it's safe to exchange secrets using it, secure in the knowledge that only this server can decrypt those secrets, and not some man-in-the-middle.
Although the public key is arguably the most important piece of a certificate, the certificate asserts quite a bit more information about the entity named in the subject. One very important piece is the validity period of the certificate itself: each certificate has a "not before" and a "not after" date. Here you can see that Amazon's SSL certificate is valid between July 2010 and July 2013. Regardless of the correctness of the signatures themselves, the certificate will be rejected if the current calendar date falls outside of this period. This is necessary because the private key that this certificate masks is used over and over to authenticate SSL connections. A very determined attacker could use details of these authentications to try to determine the value of the private key. Therefore, it's important to change the private key from time to time. The validity period not only forces the site administrator to do so, but stops an attacker who has compromised the private key from using it — if a private key were compromised, there's no way to "revoke" it, since the public key and private key are related by a simple mathematical relationship. (There's a half-solution to the problem of revoking a compromised private key in "Certificate Revocation Lists" that your browser is supposed to check before it uses a certificate, but CRL's have quite a few problems of their own).
Finally, there is a list of certificate constraints in the section labelled "X509v3 extensions". I won't go through all of these (for more information, see [4]), but one critical extension is "Key Usage". Notice that Amazon's certificate lists key usage of "Digital Signature, Key Encipherment". The issuer's certificate, however, lists key usage of "Certificate Sign, CRL Sign". The distinction is crucial to the concept of PKI. Only a certificate that has a Key Usage extension of "Certificate Sign" can "vouch for" another certificate as detailed above. In particular, Amazon can not use it's SSL certificate to sign another certificate. If they could, they could impersonate anybody! It would be trivial to generate a new certificate with a common name of, say "www.ebay.com" and sign it with the public key in the now-trusted Amazon certificate, and your browser would silently accept it.
You may have noticed, however, that this all-important key-usage section falls under a subsection title "X509v3 extensions"... indicating that there were a couple of previous versions of x509 that didn't support this extension. As it turns out, yes — PKI was actually around for quite a while before anybody noticed this gaping flaw in it's infrastructure. For this reason, most browsers will only permit a certificate "depth" (the number of certificates between the presented certificate and the root certificate) of 1 unless the key usage extension if present.
References:
- X.509 Specification
- SHA-1 Specification
- TLS 1.2 Specification
- Implementing SSL/TLS Using Cryptography and PKI
Add a comment:
Completely off-topic or spam comments will be removed at the discretion of the moderator.
You may preserve formatting (e.g. a code sample) by indenting with four spaces preceding the formatted line(s)
whole thing is signed by "Verisign Class 3 Secure Server CA - G2"'s public key and the signature is shown at the very bottom (and is even longer than the public key modulus!)
https tools.ietf.org/html/rfc5280#section-4.1
and section 4.1.1.3. signatureValue
I'm a little confused about one thing. Didn't you say the certificate is signed with the issuer public key at one point.
My understanding was the the issuer encrypts the child certificate with its own PRIVATE key and inspectors of the validity of that signature will decrypt with the issuers public key and check it's the same as the hash of the certificate they are validating?
"It would be trivial to generate a new certificate with a common name of, say "www.ebay.com" and sign it with the public key in the now-trusted Amazon certificate, and your browser would silently accept it."
Shouldn't that say "...and sign it with the private key in the now-trusted Amazon certificate..."? But browser doesn't have the private key so this problem shouldn't exist. I'm missing something.
$ openssl req -x509 -newkey rsa:512 -keyout selfsigned.key -out selfsigned.cer -subj "/CN=localhost"
keyboard shortcut:
Ctrl + Shift + i
Mac
⌘ + Option + i
How would you set up your TLS server environment to send both certs during the handshake?
As far as how to set it up, that varies from one server environment to another. This list of certificates that each sign one another up to the root is called a "certificate chain" and so the Apache server, for instance, includes an "SSLCertificateChainFile" directive which points to a PEM-encoded list of certificates.
Sir, one more thing. How can different sizes of password becomes a fixed length key in symmetrical key encryption. Example, I can set different length of password in wifi but it becomes a fixed length key (i.e. TKIP, AES). Is the password related to the AES key? As I am writing this, I was thinking that this password is being use to the DH key exchange.
Thank you very much...
I'll try to address them both here, though: there's not strictly a need for an intermediate certificate, but adding multiple layers of indirection like that protects the root certificate, which is hard to redistribute. Verisign could definitely have signed Amazon's site certificate using their root certificate, but each signature uses up a bit of the entropy in the private key, and rotating the root certificate private key would mean updating every browser.
As for the passwords and key lengths - they're (deliberately) unrelated. In SSL, for instance, the session keys, which are used in the AES encryption, are generated randomly from the pre-master secret. The pre-master secret, in turn, is derived from the shared secret that's established by the DH key exchange or the RSA key exchange.
In the case of Wifi encryption like WPA, yes. SSL doesn't actually have any authentication by default, although it does permit the option of client authentication by certificate (along with really exotic stuff like pre-shared keys).
I am little confused with this.
"Sorts the specified array into ascending numerical order.
Implementation note: The sorting algorithm is a Dual-Pivot Quicksort by Vladimir Yaroslavskiy, Jon Bentley, and Joshua Bloch. This algorithm offers O(n log(n)) performance on many data sets that cause other quicksorts to degrade to quadratic performance, and is typically faster than traditional (one-pivot) Quicksort implementations.
Parameters:
a the array to be sorted"
Thanks for this informative article. Bookmarked and will come back.
I have a question: is it possible to obtain a signature on what the server is serving? For instance, in the Amazon case, get a valid signature <em>of the HTML content</em> they are providing us?
Thanks for this informative article. Bookmarked and will come back.
I have a question: is it possible to obtain a signature on what the server is serving? For instance, in the Amazon case, get a valid signature (with Amazon's pk) <em>of the HTML content</em> they are providing us?
I am trying to create a signature with one transform validating it.but this gives me issue of "invalid digest of reference" while validating this signature.
Does the second transform mandatory to use?
Does the certificates play role in calculating the digest value?
My generated signature is:-
<dsig:Signature xmlns:dsig="/2000/09/xmldsig#">
<dsig:SignedInfo>
<dsig:CanonicalizationMethod Algorithm="/2001/10/xml-exc-c14n#" />
<dsig:SignatureMethod Algorithm="/2001/04/xmldsig-more#rsa-sha256" />
<dsig:Reference URI="">
<dsig:Transforms>
<dsig:Transform Algorithm="/2000/09/xmldsig#enveloped-signature" />
</dsig:Transforms>
<dsig:DigestMethod Algorithm="/2000/09/xmldsig#sha1" />
<dsig:DigestValue></dsig:DigestValue>
</dsig:Reference>
</dsig:SignedInfo>
<dsig:SignatureValue>Some value</dsig:SignatureValue>
<dsig:KeyInfo>
<dsig:X509Data>
<dsig:X509SubjectName></dsig:X509SubjectName>
</dsig:X509Data>
</dsig:KeyInfo>
</dsig:Signature>One suggestion: The Details about Certificate's SHA-1 hash value is calculated by hashing the tbsCertificate value is there in your reply to Jacob on 2016-03-31. It would be better if you move that to the main article.

