Understanding CRC32
Although storage space is cheap and getting cheaper, there's still a legitimate need to compress data when stored in a computer. Data compression is always a speed/space trade-off; when you compress, you use less space, but you incur a compression cost at storage time and a decompression cost at extraction time. A slightly less obvious consequence of data compression is the removal of redundancy — this is, after all, the point of compression in the first place.
The problem with removing redundancy is that even a minor corruption can be catastrophic. In computer document terms, flipping a single bit within a compressed document can render the entire document meaningless. Uncompressed data doesn't ordinarily suffer from this problem; a corruption of a single data element (say, a character in a text document) corrupts that data element but leaves the others alone. The nature of compression aims to make all the elements interdependent which does a good job of saving space but a bad job of error recovery.
The only way to deal with this is to add redundancy. As such, file compression and error recovery are actually opposing goals — however, when adding redundancy for the purposes of error recovery, the user can decide just how much redundancy is acceptable. At one end of the spectrum are what are called parity files which aim to pinpoint exactly where an error occurred - if the error checking routine knows which bit(s) are in error, they can be flipped automatically, permitting the original document to be seamlessly recovered. At the other end of the spectrum are check values, which just notify the receiver as to whether or not the document as a whole is correct. When check values are used, an algorithm is applied to the contents of the original document and the result is stored with the document itself. After decompression, the same algorithm is applied to the decompressed data and compared to the check value — if they don't match, an error has occurred, although there's no indication of where.
Check values can be fairly useful in situations where either the cost of recovering the original through other means is relatively cheap (e.g. asking the sender to re-send as in the case of a network transmission) or when space is at a premium and the risk of errors is low but not zero. Compressed files fall into the second category. If a file is compressed and stored that way, it's probably not recoverable, through any means — but bit errors on disk are rare. Still, if a file is decompressed incorrectly, the user needs to know immediately, since not all data files can be detected as incorrect by the user. Raw data - say, of monthly sales numbers - may decompress into a valid, but wrong format.
One of the simplest forms of a check value is the checksum. The checksum is easy to compute. A checksum just adds the data to be checked to a register, allowing it to overflow. A simple 8-bit checksum routine is illustrated in listing 1.
unsigned char checksum( unsigned char *in, int len )
{
unsigned char c = 0;
while ( len-- )
{
c += *(in++);
}
return c;
}
So, the checksum of the input "abcd" would be ( 97 + 98 + 99 + 100 ) % 256 = 138. Nice, neat, simple. The downside of the simple checksum is that there are a lot of errors it won't detect. For example, checksum( "dbca" ) also = 138. Although it's improbable that a storage error would shuffle the bytes themselves around, a checksum will also not detect the difference between 97, 98, 99, 100 ('a', 'b', 'c', 'd') and 96, 99, 99, 100 - and this is an entirely probable error scenario; I've just flipped the least significant bits of the first two elements. Likewise, the completely corrupt 96, 99, 98, 101 (all LSB's flipped) would checksum to the same value; 138. As it turns out, there are a whole host of errors that can occur that a simple additive overflow checksum will not detect.
Cyclic Redundancy Checks
A more robust (but more complex) check value is the Cyclic Redundancy Check (CRC). In technical terms, the CRC is the "remainder of the polynomial division modulo 2 of the input". That's quite a mouthful, so let's break that down.
Polynomial Operations
First, a polynomial is a function of a single variable which consists only of additions, multiplications and exponentiations. The canonical representation of a polynomial is:
cnxn + cn-1xn-1 + cn-2xn-2 + ... + c2x2 + c1x + c0where cn are referred to as coefficients and each individual exponent marks off a term. Thus, x5 + 3x2 + 2x + 5 is a polynomial, but sin(x)/cos(x) is not. Polynomials can be meaningfully and easily added and subtracted to and from one another; just add or subtract the coefficients of like terms. If a term appears in one polynomial but not the other, then it should be treated as having a coefficient of zero for that term. In this sense, every polynomial actually encompasses every expoenent - just that most of them have coefficients of 0.
Therefore, to say that ( 3x2 + 2x + 5 ) + ( 4x3 + 5x2 + 9x + 12 ) = ( 4x3 + 8x2 + 11x + 17 ) is to say that if you take any number x (say, 3), and evaluate ( 3(3)2 + 2(3) + 5 ) = 27 + 6 + 5 = 38, ( 4(3)3 + 5(3)2 + 9(3) + 12 ) = 108 + 45 + 27 + 12 = 192, then ( 4(3)3 + 8(3)2 + 11(3) + 17 ) = 108 + 72 + 33 + 17 = 230 = 38 + 192, which it does. This all follows intuitively from the nature of addition.
Likewise, polynomials can be multiplied. In this case, though, you don't combine like terms but instead multiply every combination of terms between the two polynomials by one another. Since multiplying powers just adds exponents (after all, x5 * x2 = xxxxx * xx = xxxxxxx), multiplying terms involves multiplying the coefficients and adding the exponents. This can work out to quite a few operations - one helpful way to keep track of them is to line them up, just as you probably learned to do with numerals in elementary school:
4x3 + 5x2 + 9x + 12
* 3x2 + 2x + 5
20x3 + 25x2 + 45x + 60
8x4 + 10x3 + 18x2 + 24x
12x5 + 15x4 + 27x3 + 36x2
12x5 + 23x4 + 57x3 + 79x2 + 69x + 60
Polynomial Division
Second, just as polynomials can be added, subtracted, and multiplied, they can also be divided. This is easy enough to describe, although can be a bit tedious to carry out by hand - just invert the multiplication.
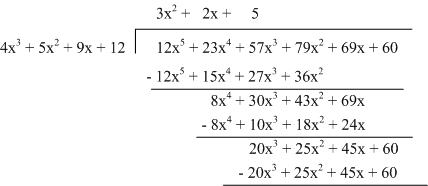
Algorithmically, this means first dividing the left-most term of the divisor by the left-most term of the dividend. Looking back at the multiplication in example 1, you can see why - the left-most term of the product is the product of the left-most terms of the multipliers. Divide these to get the first term of the quotient, 3x2. Now recover the last row of the multiplication by multiplying 3x2 by each term in the dividend:
12x5 + 15x4 + 27x3 + 36x2
And subtract these terms from the divisor:
8x4 + 10x3 + 18x2 + 24x
Now, divide the left-most term of the dividend by the new left-most term to get 2x; multiply out, subtract, and continue. In this way, you've discovered a polynomial which can be multiplied by the dividend to yield the multiplier.
This is tedious to do by hand and, being so algorithmic, cries out for a code solution. Listing 2 illustrates a straightforward implementation of polynomial division in C. Polynomials are stored as arrays of doubles; the position in the array implies the exponent. Thus if array[2] = 3.0, then the coefficient of the x2 term is 3. This means that polynomials are stored "backwards", but makes the implementation a bit easier to follow.
int divide( double num[], int nlen,
double den[], int dlen,
double quotient[], int *qlen )
{
int n, d, q;
// The lengths are one more than the last index; decrement them
// here so the call is less confusing
nlen--;
dlen--;
q = 0;
// when n > dlen, the result is no longer a polynomial
// (e.g. trying to divide x by x^2
for ( n = nlen; n >= dlen; n-- )
{
// First, divide the nth element of numerator with the last element
// of the denominator
quotient[ n - dlen ] = num[ n ] / den[ dlen ];
q++;
// Now, multiply each element of the denominator by each
// corresponding element of the numerator and subtract the
// result
for ( d = dlen; d >= 0; d-- )
{
num[ n - ( dlen - d ) ] -= den[ d ] * quotient[ n - dlen ];
}
}
*qlen = q;
return ( nlen - *qlen + 1 );
}
This routine, although far from perfect, illustrates polynomial division — I'm using the terms num(erator) and den(ominator) instead of dividend and divisor since they both start with divi, which would make the code a bit difficult to read. The quotient is returned, along with its length, in the last two parameters. This is meant to be called as shown in listing 3.
double num[] = { 60.0, 69.0, 79.0, 57.0, 23.0, 12.0 };
double den[] = { 12.0, 9.0, 5.0, 4.0 };
double quot[ 3 ];
q = sizeof( quot ) / sizeof( double );
divide( num, sizeof( num ) / sizeof( double ),
den, sizeof( den ) / sizeof( double ),
quot, &q );
(Recall when reading listing 3 that polynomials are stored "backwards").
Just as when dividing integers, though, it's entirely possible to divide one polynomial by another one that doesn't divide evenly; if you do this, there's a remainder left over. In the case of polynomial division, this is what's left over of the divisor after all of the subtraction operations have been successfully carried out. This remainder is actually the point of interest for the CRC. The polynomial division algorithm in listing 2 returns the remainder by modifying the numerator itself; the return value of the function is the length of the remainder.
Polynomial division modulo 2
Third, this polynomial division is carried out modulo 2. What this means is that every coefficient should be divided by 2 and the remainder of this division used instead of the coefficient itself. What this practically amounts to is that every coefficient must first either be 1 or 0, and the addition operation changes to:
| a | b | a + b | ( a + b ) % 2 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 2 | 0 |
| a | b | a - b | ( a - b ) % 2 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | -1 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
Changing the polynomial division routine in listing 2 to work modulo 2 requires only a one line change:
for ( d = dlen; d >= 0; d-- )
{
num[ n - ( dlen - d ) ] -= den[ d ] * quotient[ n - dlen ];
num[ n - ( denlen - d ) ] = fabs( num[ n - ( denlen - d ) ] );
}
And listing 4 is now a working CRC calculator. To compute a CRC, turn the input into a very long polynomial by making each bit into a coefficient. So, if the input was 20 bytes long, the highest order coefficient would be x20 * 8 = 160. This is divided by a fixed polynomial and the remainder of this division is stored with the compressed result. The decompressor computes the remainder of the uncompressed data with the same fixed polynomial; if they match, then the data uncompressed correctly.
The CRC is specifically designed to catch errors that a simple checksum won't. Specifically, depending on the structure of the fixed divisor, the CRC algorithm is particularly attuned to long strings of 1's or 0's inserted into an otherwise correct bitstream — these will be detected with high probability. This is important, because this is exactly the sort of thing that tends to occur in noisy channels.
The most common CRC divisor value is the CRC32 which is the polynomial x32 + x26 + x23 + x22 + x16 + x12 + x11 + x10 + x8 + x7 + x5 + x4 + x2 + x + 1. To compute the CRC32 of the input 'ABC', you would call it as shown in listing 5.
int q;
double q32[ 32 ];
double crc32[] = { 1.0, 1.0, 1.0, 0.0, 1.0, 1.0, 0.0, 1.0,
1.0, 0.0, 1.0, 1.0, 1.0, 0.0, 0.0, 0.0,
1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0,
0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0 };
double ABC[] = { 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0,
0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0,
0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0,
0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0,
0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0, // C
0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, // B
0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0 // A
};
r = divide_crc( ABC, sizeof( ABC ) / sizeof( double ),
crc32, sizeof( crc32 ) / sizeof( double ),
q32, &q );
Notice that I have to pad the 24-bit input with an additional 32 bits of zeros; otherwise, the remainder of the division operation would just be the CRC32 itself (and the quotient would be 0). The binary values for A, B & C (65, 66 & 67) appear backwards here because (if you recall) the polynomial array is loaded "backwards" with the coefficient for x0 in the first position.
Example 3, below, illustrates the computation of the CRC32-value of "ABC". At each point in the division, the important piece is shown in bold; this is the current CRC32 — the remainder of the polynomial division. The final value is 01011010010110110100001100111010, or 0x5A5B433A. (This still doesn't match the official specification - I'll detail why, and correct this, in must a moment).

Efficient CRC Computation
You're probably cringing at the amount of memory and time this straightforward implementation wastes - an array of doubles to hold ones and zeros? I'm sure you've already spotted an obvious optimization: store the polynomials themselves as bits. If you do this, you can make a further speed optimization — you likely noticed that tables 1 and 2 are actually the logic tables of the XOR operation, which can be carried out much faster by a microprocessor than subtraction operations. Since the quotient itself is not needed, there's no reason to store it — the only important part of the calculation is the remainder. Listing 6 is a sleek, simple, streamlined implementation of the CRC calculation shown in listing 4. The results are equivalent, but this implementation is much faster and memory efficient.
unsigned long int compute_crc( unsigned long input,
int len,
unsigned long divisor )
{
while ( len-- )
{
input = ( input & 0x80000000 ) ? divisor ^ ( input << 1 ) : ( input << 1 );
}
return input;
}
...
unsigned long int crc32_divisor = 0x04C11DB7;
unsigned long int input = 0x8242C200; // ABC; backwards & left aligned
printf( "%lx\n", compute_crc( input, 24, crc32_divisor ); // 5A5B433A
If you've been following along very closely, you may have noticed that the CRC32 divisor has a coefficient at x32 — which means that it's actually 33 bits long, one bit too long for a long integer. So how can you represent it in a 32-bit int? You don't. The CRC32 check value is 32 bits long, so the most-significant bit in the divisor doesn't factor into the computation at all. It's actually just there in the specification to clarify that the divisor is 32 bits long, rather than 26. The bit at x32 actually never factors into the computation. The divisor of 04C11DB7 above, therefore, just omits it entirely.
There are two glaring problems, though, with the routine in listing 6. The first, and most obvious, is that it can only compute the CRC of a maximum of 32 bits of input. The second is that I've replicated the bit ordering of listing 4. Although this makes listing 4 easy to read, it complicates the loading of the input, since you have to specify everything "backwards" — if you want to compute the CRC of "ABC", you have to reverse the bits and left align them to match the endian-ness of the processor. Listing 7 reverses the computation so that bytes are processed in the correct order, and accepts an array of arbitrary length, processing the input one byte at a time.
unsigned long int compute_crc( unsigned char *input,
int len,
unsigned long divisor )
{
int i, k;
unsigned long crc = 0x0;
for ( i = 0; i < len; i++ )
{
crc ^= ( input[ i ] );
for ( k = 8; k; k-- )
{
crc = crc & 1 ? ( crc >> 1 ) ^ divisor : crc >> 1;
}
}
return crc;
}
A more subtle problem with the CRC computation in listing 7 is that it doesn't "kick in" until the first 1 bit in the input. This may not necessarily seem like a significant problem, but this means that an input prepended with a run of leading 0's will not be detected as an error by the CRC computation. For this reason, the official CRC32 standard suggests that you start with all 1's instead of all 0's - listing 8, then, shows how to compute the actual correct, official, CRC32 according to the standard. The output of this will match any other "proper" standard-compliant implementation. Also note that since the processing has been reversed, the CRC divisor has to be as well - the correct CRC32 divisor for the routine in listing 8 is 0xEDB88320.
unsigned long int compute_crc( unsigned char *input,
int len,
unsigned long divisor )
{
int i, k;
unsigned long crc = 0xFFFFFFFF;
for ( i = 0; i < len; i++ )
{
crc ^= ( input[ i ] );
for ( k = 8; k; k-- )
{
crc = crc & 1 ? ( crc >> 1 ) ^ divisor : crc >> 1;
}
}
return crc ^ 0xFFFFFFFF;
}
...
printf( "%lx\n", compute_crc( "ABC", 3, 0xEDB88320 ); // a3830348
You can make a space/speed tradeoff and speed up this routine even more. The key observation here is that the CRC32 of a single byte doesn't change from one run to the next - so you can pre-compute the values of each possible input byte and store them in memory. Take a look at listing 9; here the CRC32 of each byte is computed individually and the byte values are concatenated together to compute the final CRC value.
unsigned long int crc_byte( unsigned long input,
unsigned long divisor )
{
int k;
for ( k = 8; k; k-- )
{
input = input & 1 ? (input >> 1) ^ divisor : input >> 1;
}
return input;
}
unsigned long int compute_crc( unsigned char *input,
int len,
unsigned long divisor )
{
int i;
unsigned long crc = 0xFFFFFFFF;
for ( i = 0; i < len; i++ )
{
crc = crc_byte( ( crc ^ input[ i ] ) & 0xff, divisor ) ^ ( crc >> 8 );
}
return crc ^ 0xFFFFFFFF;
}
This isn't any faster than the implementation in listing 9, but the invocation of crc_byte can be replaced with a call to a lookup array as in listing 10, which speeds things up quite a bit.
unsigned long crc_table[ 255 ];
unsigned long int compute_crc( unsigned char *input,
int len,
unsigned long divisor )
{
int i;
unsigned long crc = 0xFFFFFFFF;
for ( i = 0; i < len; i++ )
{
crc = crc_table[ ( crc ^ input[ i ] ) & 0xff ] ^ ( crc >> 8 );
}
return crc ^ 0xFFFFFFFF;
}
...
for ( i = 0; i < 255; i++ )
{
crc_table[ i ] = crc_byte( i, crc32_divisor );
}
In fact, most CRC implementations use a table like this one and don't even compute them at startup time but instead hardcode them as illustrated in listing 11.
/* ========================================================================
* Table of CRC-32's of all single-byte values (made by makecrc.c)
*/
ulg crc_32_tab[] = {
0x00000000L, 0x77073096L, 0xee0e612cL, 0x990951baL, 0x076dc419L,
0x706af48fL, 0xe963a535L, 0x9e6495a3L, 0x0edb8832L, 0x79dcb8a4L,
0xe0d5e91eL, 0x97d2d988L, 0x09b64c2bL, 0x7eb17cbdL, 0xe7b82d07L,
...
Listing 11 is, in fact, an excerpt from Jean-loup Gailly's CRC implementation in the open-source gzip application. Listing 10 is, more or less, how he implemented the actual CRC computation.
Add a comment:
Completely off-topic or spam comments will be removed at the discretion of the moderator.
You may preserve formatting (e.g. a code sample) by indenting with four spaces preceding the formatted line(s)

